Depth First Search & Minesweeper

I stumbled upon Ruby2D this week. When I learned both Ruby-Processing and Gosu the first thing I implemented was a simple Minesweeper game. Ruby2D is still under development, but it has enough functionality for me to build Minesweeper. Within a few hours, I had a basic game working.

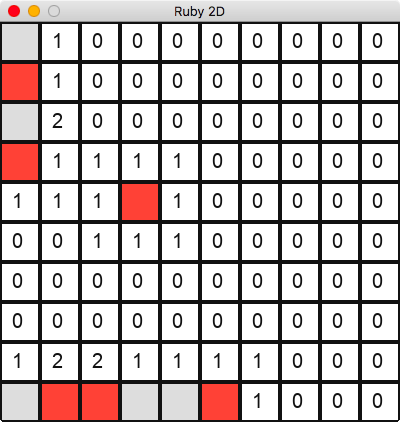
In Minesweeper, when you click on a square the game reveals the number of mines nearby. If there aren’t any mines nearby, the neighboring squares are revealed. If those squares do not have any mines nearby, the process is repeated until you get to a square that has a mine nearby. This behavior, a progressive reveal until you get near a mine, is the trickiest part of implementing the game. The first two implementations I tried didn’t work. Then I remembered, when I implemented Minesweeper in college I used depth-first search for the progressive reveal. Using depth-first search, I finished my Ruby2D version of Minesweeper.

Depth-first Search

So what is depth-first search? It is an algorithm for exploring a graph, a tree, or another data structure in a systematic way. In a depth-first search, you go as far in any direction you can before backtracking and trying a different direction.

If you have ever solved a maze by following along a wall you’ve used depth-first search. I know several folks who use this technique when playing first person shooter video games. They explore new levels by always going right when they come to an intersection. When they hit a dead end they double back and try a different path. With computers, people often explain depth-first search using trees like this one.

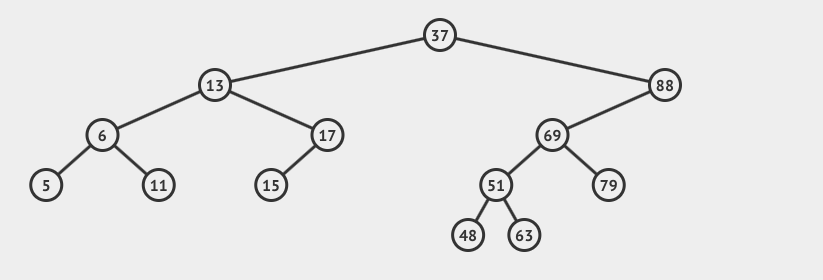
To traverse or search this tree using depth-first search you start at the top, at 37. You then go left until you hit a place where you must make a choice, and then again you take the left branch. The first four numbers I visit are 37, 13, 6, and 5 in that order. There are no paths branching off of 5, so I backtrack to 6 and then go right visiting 11. 11 also has no paths branching off of it, so I go back again to 13 and explore 17 which I had skipped on my way down. Following this pattern the depth-first search of this tree visits each number in the following order: 37, 13, 6, 5, 11, 17, 15, 88, 69, 51, 48, 63, 79.

Notice that you only record a number the first time you visit it. If the number is visited again, while backtracking, you do not count that visit.

Wait, Wasn’t This About Minesweeper?

So how does this relate to Minesweeper? Minesweeper does not have anything that looks like a tree. It turns out you can still use depth-first search when revealing squares after a player’s click. When the player clicks on a square with no mines nearby, I reveal that square. Then I check to see if the square above it has any mines nearby. If it does not, I check the square above that one and so on until I find a square with mines nearby. After I find a square with mines nearby I check all of its neighbors, (upper right, right, lower right…) going clockwise until I find a neighbor without any mines nearby (value 0) and then making that one my current focus. Here is the pseudocode.

reveal x, y
  focus = square at x, y

  if focus at x, y has no nearby mines
    check each neighbor of the focus
    if a neighbor has no nearby mines
       reveal neighbor  (recurse!)

Here is what it looks like, in Ruby, in my game.

def reveal x, y
  s = @squares[x][y]

  return if s.revealed?

  s.reveal

  return if s.mine_nearby?

  neighbors = neighbors x, y

  until neighbors.empty?
    reveal *to_check.pop
  end
end

On line 4 I do one thing I did not mention above. If a square is already revealed I do not reveal it again. I did this to prevent infinite loops. Infinite loops don’t happen when doing a depth-first search of a tree but they can occur iwith Minesweeper.

Conclusion

That is all there is to depth-first search. Implementing it requires very little code, and it is an algorithm many of us already use for solving mazes or playing video games. There are more efficient search algorithms, but many of them start with depth-first search and modify it to be more effective. I will cover those algorithms in later posts.